Коментари към решението на петата задача
В.Молотков
1. Наивния алгоритм.
Когато човек ще види условието на задача, първите неща които се забелязват веднага
са:
1. Функцията f(P)=min{distance(P,Pi)} чийто максимум
се терси, е гладка навсякъде, освен крайно множество от прави линии, всяка една
от които е еквидистантна на някоя двойка точки на многоъгълника (тъкмо тези прави
се наричат "симетрали" в авторското решение). При това функцията f е гладка в околността
на всяки един връх Pi на многоъгълника, и точките Pi
са единствените точки, където функцията достига локален минимум. По този начин равнината
се разбива на N свързани отворени (и изпъкнали) области.
2. Там, където функцията е гладка, тя няма максимум, дори и локален.
3. Оттук следва, както е отбелязано в авторското решение, че точката, в която максимума
се достига, може да бъде само:
а) Един от върховете на ограничаващ правоъгълник;
б) точка на пресичане на една от симетралите със една от страните на правоъгълника;
в) точка на пресичане на някои две от симетралите (но само ако тя е вътре в многоъгълника).
А по-точно, център на окружността, породена от някоя тройка Pi,Pj,Pk
на върховете на многоъгълника.
Докато върхът на правоъгълника с максимално разстояние до многоъгълника, както и
самото максимално разстояние се намира елементарно още в процеса на четенето на
входния файл (и може да служи по-нататък за филтриране на неперспективни точки от
класа б) ("външни") и в) ("вътрешни")), практични алгоритми за намиране на оптимални
точки от класове б) и в) са наистина доста засукани. Праволинеен алгоритм за намиране
на оптималната вътрешна точка, директно следващ от горните наблюдения, може да бъде
формулиран по следния начин: разгледай всички окръжности, породени от произволни
тройки точки на многоъгълника и не съдържащи вътре никой от върховете на многоъгълника;
избери измежду тях тази с най-голям радиус. Този алгоритм е, очевидно, със сложност
O(N^4), което при N==1000000 е умряла работа. Също така
се вижда, че brute force алгоритм за намиране на външна оптимална точка има сложност
O(N^3), защото в него участва множество от двойки върхове на многоъгълника
вместо множество от тройки.
2. Диаграмите на Вороной -- що е то?
Свързаните области на гладкост на функцията f са известни под името
области на Вороной. А обединение на границите на затворена обвивка на тези области
-- това е диаграмата на Вороной. Тя състои от отрязеци на прави и полуправи (парчета
от симетралите разгледани горе). Този факт, (т.е. че говоря проза :-)), открих вчера,
медитирайки над картинката на третата страница на препоръчаната от автора на задачата
статия wwwpi6.fernuni-hagen.de/Publikationen/tr198.pdf.
Какво отношение те биха могли да имат към задачата? Да предположим, че съответната
диаграма за нашия многоъгълник е изчислена, като заедно с всеки връх V
на диаграма е зададен и списък (PV1...PVn) на
точките на многоъгълника, намиращи се на минимално разстояние от този връх (за нас,
всъщност е достатъчна само по една точка от всеки списък). Тогава, очевидно, искомата
оптимална вътрешна точка P е този от върховете V който
максимизира distance(V,PV1). Това ни дава алгоритъм с ефективност
O(algorithm for Voronoi diagram)+O(NV), където NV
е числото на върхове на диаграмата на Вороной. Забележителен факт е
, че както NV, така и броя на ребра на диаграмата на Вороной
(те са нужни за намиране на оптималната "външна" точка) е по-малък или близо до
6*N (Lemma 2.3 на стр.5 от горецитираната статия). Тъй че, ако имаме
кода на достатъчно ефективен алгоритм за изчисляване на диаграмите на Вороной, работата
ни е в кърпа вързана! Обаче, има ли такива кодове в Internet?
3. Търсене в Internet и експерименти с кода.
При търсене в Internet открих 3 сорса, писани на C: Qhull, кода на Fortune (използван
от 4-ма участници в конкурса ;-)) и кода от библиотеката Leda. Имаше сорсове и на
Java, но често пъти те са буквален плагиат на съответните сорсове на C/C++ (без
посочване на авторите), тъй че тях аз не ги гледах. Аз направих тестове с Qhull
i Fortune (по-точно с програмата на Иван Попов, в която Fortune е вградено без бъгове,
за разлика от тритте други програми исползващи Fortune). А що се отнася до Leda:
отдавна се каня да компилирам библиотеките на free версия на Leda (v.3.2.3), но
все не намирам време. Тъй че тествах само Qhull и Fortune.
Резултати от тестовете:
1. Qhull Този пакет имам го от времето на миналия конкурс. Той е с универсално
предназначение: намира изпъкнали обвивки, диаграми на Вороной, Делоне триангулации,
и т.п, и то в многомерни пространства. Както се твърди от авторите му -- много ефективно.
Което не е лъжа, поне що се отнася за изпъкнали обвивки на големи случайни множества
от точки [1].
Този път пуснах съответната програма (qvoronoi.exe) с модифицираните за целта тестови
файлове. Програмата бързо премина тестове 1--7, тест 8 и отне 2 сек., тест 9 --
18 сек., а тест 10 -- цели 242! [2].
Да пускам и останалите два теста нямаше смисъл.
1. Fortune Тест 8: 0.55 сек, тест 9: 35 сек, тест 10: 92 сек. Т.е. Fortune
е 2 до 4 пъти по-бърз от Qhull, ако се изключи 9-ти тест, където той е 2 пъти по-бавен.
Както и да е, нито една от дветте програми не може да се справи с тестове от 9 нагоре.
Тъй че, post factum, моето незапознанство с диаграмите на Вороной по време на писането
и обмислянето на решението се е оказало добро -- иначе здравата бих загазил. [3].
4. Моя алгоритъм.
При алгоритмите основани на диаграмите на Вороной при намирането на оптималната
точка няма разлика между "вътрешни" и "външни" точки, ако към върховете на диаграмата
на Вороной се добавят и точки на пресичането на нейните ребра с контура, заедно
със съответните минималните разстояния.
Моя алгоритм обаче се разцепва на два подалгоритма. Един от тях, реализиран в функцията
MaxPerim(), намира (или, по-скоро, би трябвало да намира :) оптималната
"външна" точка, докато другият, реализиран в "дървена" рекурсивна функция MaxCircle(...)
намира "вътрешна" такава. Ще ги разгледаме последователно.
A. Намиране на "външния" оптимум.
На пръв поглед всичко тук е просто: Разглеждаме всички двойки (Pi,Pi+1)
на последователни точки от входния файл (факта, че входа е нареден counterclockwise
е добре дошел тук), намираме пресечната точката Qi на тази
полуправа от симетрала на Pi,Pi+1, която е външна
спрямо многоъгълника, със граничен контур, изчисляваме разстоянието между Qi
и Pi и избираме максималното измежду тези разстояния (вж.картинката
отляво, където в точката P се достига "външния" оптимум, а в точката
Q -- "ъгловия"). Ако "ъгловото" максимално разстояние (синята линия
на рисунката) е по-голямо или равно на "външното" максимално разстояние (всяка една
от дветте зелени линии), всичко е OK; същото е в случая, ако многоъгълника е достаточно
"дебел". Вместо да давам формално определение, какво значи това, по добре да нарисувам
една друга картинка, от която нещата стават ясни: 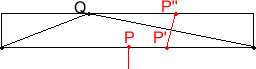 където
където N==3, а P е "оптималната" точка, намерена в съответствие
с горния алгоритм. Вижда се с невооръжено око, че P в същност не е
оптимална. Причината за това явление е очевидна из картинката: едната от точките
на (много)триъгълника - Q - е по-близо до P, отколкото
другите две. В този случай в играта встъпват и точките на пресичане на някои от
"вътрешните" (т.е. пресичащи се с вътрешността на многоъгълника) полу-симетрали
с контура (точката P' от картинката). Нещата могат да станат и още
по-гадни, както се вижда от следващата рисунка:
T.e. в общия случай може да се наложи да разгледаме симетрали не само на съседните
точки в многоъгълника, но и на произволна двойка такива точки, при което алгоритма
става O(N) пъти по-сложен. [4]. От гореизложеното
се очертава следния алгоритм:
0. Образуваме една приоритетна опашка Queue от тройки (P,r,index),
къдъто P точка, r -- радиус, а index -- променлива
от тип int; опашката ще е подредена по радиус (големи радиуси -- в
главата и)
1. Слагаме в опашката всички тройки (Qi,ri,i),
такива че Qi е точката на пресичане на външна полу-симетрала
на двойката (Pi,Pi+1) със контура, ri
е разстояние от точката Qi до точката Pi
и ri > максимално "ъглово" разстояние. От гореизложеното
е ясно, че външното оптимално разстояние не може да бъде по-голямо от радиуса на
тройката намираща се в главата на опашката.
2. Повтаряме следните стъпки:
а) Изваждаме тройката (Q,r,index) от главата на опашката;
б) Ако index==-1 връщаме двойката (Q,r) като резултат;
в) В противен случай гледаме, дали има точка Pi, намираща
се вътре в окръжността с център Q и радиус r. Ако не --
връщаме двойката (Q,r) като резултат;
В противен случай образуваме масив Internal от всички такива лоши точки
(+точките Pindex и Pindex+1 лежащи
на самата окръжност), след което разглеждаме всички двойки (P,P') точки
от масива Internal, построяваме точката на пресичане Q'
на "вътрешна" полу-симетрала на двойката (P,P') с контура и т.н. и
т.н. (опускам очевидни но утомителни за описание детайли). Най-накрая избираме Q',
такова че r'=distance(Q',P) да е максимално, и поместваме тройката
(Q',r',-1) в опашката Queue.
Сложността на скицирания алгоритм за най-лошия случай [5].
е О(N^3*log(N)), т.е. е още по-лоша от тази на brute force алгоритм,
но за "масовите" случаи тя е доста по-малка, като за най-простите е от порядъка
на О(N*log(N)) Всъщност аз успях да реализирам само един евристичен
вариант на най-сложната стъпка 2в) от гореописания алгоритм, като търсих "лоши"
за тройката (Q,r,index) точки само в околността на онова ребро на многоъгълника,
което е "антипод" на реброто (Pindex,Pindex+1);
освен това разглеждах само тези двойки от лоши точки, които са съседни в многоъгълника,
т.е. изключих възможността на ситуацията изобразена на картинката горе. И всичко
това го писах в страшна терапана, за час и половина до изтичане на deadline, в резултат
на което вероятността този код да е безбъгов е близо до нула. За щастие, само в
двама от тестовете (9 и 12) оптималната точка лежеше на границата на правоъгълника.
И в двата случая многоъгълниците бяха "дебели", тъй че съответните бъгове нямаха
възможност да се развихрят :-))).
Б. Намиране на "вътрешния" оптимум.
1. Основна идея: scaling. Да предположим, че нашия многоъгълник има много точки
(на картинките долу, всеки пиксел на елипса е точка от многоъгълника). Ще се опитаме
да намерим оптималната точка по следния начин.
1). Ще създадем локален масив Pi[] от "разредени" върхове на многоъгълника,
като ще игнорираме точки, коитo се намират "прекалено близо" до предишната точка
в масива. Това се регулира от параметър scale, който пък еднозначно се определя
от максимален брой точки, които искаме да исползваме в началния стадий на алгоритма,
за грубото първо приближение (константата MAX_POINTS, която е 128 в реалния код,
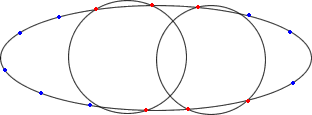
и 16 на картинката долу). На лявата рисунка долу в този масив има 14 точки (оцветени
в синъо и червено). Намираме -- с brute force алгоритм, но малко число точки-- "максималните"
с някоя точност epsilon=0.0000005 окръжности, кандидатстващи за званието "оптимална",
които поместваме в една приоритетна опашка (дветте окръжности от лявата рисунка
долу). Стойността на константата epsilon е напипана емпирично, с оглед да се избегне
както прекалено голям брой окръжности, оцеляли в опашката, така и някои бъгове (с
не напълно ясен произход >:((), възникващи при изчисленията с double (или long double).
2). Намаляваме параметра scale: scale/=2 и повтаряме процедурата 1)
за всяка от окръжностите C от опашката от по-горното ниво. Като в разреден
масив Pi[] поместваме само точките, които са вътре в C
-- пак с точност epsilon. Дясната картинка долу илюстрира опашката
от окръжности от второ ниво (червени), получаващи се при "детайлизиране" на лявата
окръжност от ниво 1. При все това запазваме, разбира се, и най-добър "глобален"
кандидат за оптималната окръжност.
3). Излизаме от процедурата, когато scale ще стане толкова малък, че разреждането
няма да го има вече. По-абстрактно казано, алгоритм построява рекурсивно едно дърво
от изглеждащи "хубави" при дадено увеличение на микроскоп (т.е. параметр scale)
окръжности, претендиращи за оптималност и осъшествява търсене в дълбочина. Заради
тази "дървеност" теоретичната му ефективност се определя трудно, но практически
(т.е. за "масовия" случай) не е лоша (вж. обаче коментар [6]).
Друг е въпрос, дали алгоритъм е евристичен, или може, след изчистването на останалите
бъгове да се превърне и в точен. На този въпрос аз не зная отговор засега.
 |
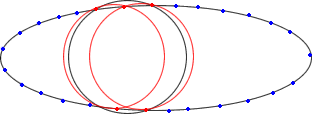 |
| Scaling at depth 1 |
Scaling at depth 2 |
2. По-важни детайли.
1. За да бъде една окръжност с достатъчно голям радиус поместена в опашката като
"хубава", тя, освен всичко друго трябва да бъде максимална в смисъл, че не може
да се увеличи нейния радиус с малки деформации, такива че по време на тази деформация
нито един връх на многоъгълника не влиза вътре в окръжността. Дефиниция на това,
какво точно значи "малка деформация" е "дълга и широка", но интуитивно е ясно, че
такива неразширими окръжности са в точност тези, които са породени от точки, образуващи
остроъгълен триъгълник. Трябва да се включи и граничен случай на правоъгълните
триъгълници (иначе ще бъдат игнорирани правоъгълниците!). А тъй като всички сравнения
от типа X <= Y трябва да се провеждат "с точност до epsilon"
(за разлика от изчисления с плаваща запетая, провеждани с максимална възможна тожност),
някое число от "почти правоъгълни" триъгълници с тъп ъгъл попадат в съответните
приоритетни опашки. Което е довело до един мръсен бъг, присъстващ в тестваната версия:
"изчезването" на някои от такива окръжности от приоритетна опашка при двойно намаляване
на параметра scale. Безуспешното търсене на причините за този бъг (който
ме е лишил от 2 точки) ми е отнело почти една седмица по време на писането на кода,
а едноредов bug fix го открих само преди няколко дена: ред 413 от моя сорс "fire.cpp"
трябва да се замени с
return MaxCircle(depth-1,c0,scale/2);//"No circle" bug fix (30.3.02)
2. Друг важен момент: коректна работа с некоректните "плаващи" числа. Имаше едно
явление, което ме тормозеше много: при изчисляването (по известни формули от училището)
на цънтъра на окръжността породена от един триъгълник с много остър ъгъл грешката
е била много голяма -- някъде в 4-ти или 5-ти знак след запетайката (дори при изчисления
с long double!), което при по-малки epsilon пак довеждаше до неприятни
явления с изчезването на окръжности при увеличаване на дълбочината на рекурсия.
Ще напомня, че epsilon, параметър на точността на сравнения; при неговото
увеличаване до размера на грешките при изчисляване на центъра на окръжността, броя
на окръжности в опашките се увеличаваше многократно, драстично намалявайки скоростта
на алгоритма.
Тъй че за по-точното намиране на центровете аз използвах след "училищните" изчисления
и една quicky (в смисъл, написана бързо на ръка :) версия на метода на последователни
приближения. Разбира се по-добре би било вместо това просто да се търси пресечката
на симетрала на най-късата страна на триъгълника с симетрала на най-дългата му страна,
защото големите грешки при малки ъгли възникват тъкмо заради това, че се търси пресечката
на две почти успоредни линии. Обаче заради терапаната (писах този коригиращ код
в последния ден вечерта, няколко часа преди изтичане на срока) написах това, което
написах.
3. Изпъкналостта на многоъгълника играе в този алгоритм много важна роля. Тя позволява
да прецени за една перспективна окръжност C с радиус radius
(и построена от "разредени" точки), долната граница inf(radius) на
радиусa на максималната "хубава" окръжност която може да се построи от всички
(т.е. неразредени) точки на многоъгълника съдържащи се вътре в C. Така
че, ако inf(radius) е по-голямо (с точност epsilon) от
радиус на окръжността в главата на опашката, опашката се изпразва, след което в
нея се помества окръжност C. Съответния параметр delta
за намиране на тази долна граница (inf(radius)=radius-delta) аз го
изчислих по една приближена формула delta=scale*scale/(radius*2) .
Тази формула е добра, когато ъгъла delta=scale/radius е малък (какъвто
е масовия случай), обаче понякога той може да се окаже голям, както аз открих преди
няколко дена! Подозирам, че това е причина поне за някои от оставащи все още бъгове.
А точната формула (с sin и cos) беше нетрудно да се напише,
но ми беше мързел (и все още е :).
5. Коментари към "авторското" решение.
1. Авторското решение с hill climbing, т.е. решението описано във авторския анализ
на задачата, възможно би могло да се приложи успешно за намиране на максимума (минимума)
на непрекъсната функция f ако тази функция би била вдлъбната (изпъкнала),
или, по-общо, би имала само един локален максимум(минимум), който едновременно е
и глобален. Тъкмо такъв бе случая с 6-та задача от миналогодишния конкурс [1],
където аз използвах една по-канонична разновидност на този метод (в смисел че е
описана във всички учебници :) известна под кодово име subgradient method. При този
метод: началната точка P се избира горе-долу произволно, но желателно
да е в околността на центъра на тежестта (както и в авторското решение); вместо
М точки се избират М единични вектори (направления)
n1,...nM. След това се избира направление ni,
такова че разликата d=f(P+epsilon*ni)-f(P) е максимална
(минимална). Тук epsilon е исканата точност. Ако модула на това максимално
d е по-малък от epsilon, значи P е оптимална
с зададена точност. В противен случай намираме точката P' на права,
минаваща през P в направление ni на най-бързото
качване (спускане), в която функцията f, а по-точно нейното ограничение
върху правата е оптимално. Полагаме P=P' и продължаваме цикла. Максимума
върху правата се намира както е описано в авторското решение, с тези разлики че
а) възможните направления в едномерния случай са само две и б)вместо с "голяма",
но невъзрастваща (както е в авторското решение) стъпка S, се започва
с "безкрайно малка" стъпка S=epsilon, като стъпката всеки следващ
път се удвоява (или, по-добре се умножава със "златното сечение" 1.618),
докато е възможно. Тогава интервал между последната и предпоследната точки на правата
съдържи оптималната за тази права точка, която след това стесняваме този интервал
с дихотомии: разделяме го на два равни подинтервала (или, по-добре, в отношение
1:1.618 -- пак "златното сечение"), определяме, в кой от тях се намира оптималната
точка, и т.н., докато модул на разликата на целевата функция |f(P0)-f(P1)|
в началото и в края на интервала (не дължината на интервала!) ще стане по-малък
от epsilon.
Тези малки разлики довеждат до това че subgradient method е със сложност O(log(D/epsilon))
и в най-лошия случай, докато hill climbing гарантира само O(D/epsilon)
(D е разстоянието между началната и оптималната точки). Да речем, ако
областта, в която се търси оптимум е правоъгълник 1М*1, тогава не може да се избере
начално S по-голямо от 1. И ако 1М-2 точки се намират на левия край
на този дълъг правоъгълник близо една до друга и само две точки -- в ъглите на десния
край, то центъра на тежестта се намира около ляв край, оптимална точка -- по средата,
(като на рисунка:  ) и алгоритм ще трае ) и алгоритм ще трае 1М*0.5М=5*10^11*средно
време на елементарна операция T.e. 500 сек. на 1G процесор, ако средна елементарна
операция се извершва за един такт -- което е далеч от реалността :-).
2. Обаче всичко казано горе важи само за хубавите функции, с единствен локален
и глобален максимум. Колко такива локални максимуми може да има в нашата задача?
Отговор: число от порядъка O(N): лесно се вижда, че в термините на
диаграмите на Вороной, всеки локален минимум се намира във един от върховете на
диаграмата на Вороной. Обратното не е вярно: в тъпоъгълен триъгълник единствен връх
на диаграмата на Вороной (пресечна точка на тритте симетрали) не е точка на локален
максимум, т.е. за такъв триъгълник локален максимум изобщо няма. Тъкмо това бе и
причината, заради която аз изключих в алгоритма ми такива триъгълници при намирането
на "вътрешна" оптимална точка. А сега примера, илюстриращ случая, когато локалните
максимуми са много:  (червените точки на картинката).
От тази картинка се вижда също така, че както "авторския", така и "каноничен" вариант
на метода на най-бързото качване яко ще се издъни на този простичек пример: точката
на локалния максимум в която алгоритм ще се приземи силно зависи от точката на старта
му. Ако се стартира от "цънтъра на тежестта" (синята точка), ще бъде върната
като оптимална една от дветте съседни червени точки, докато същинския оптимум очевидно
е най-лявата такава. Вижда се също така, че условието за единственост на оптималната
точка по никакъв начин не помага в намирането на точка от (червените точки на картинката).
От тази картинка се вижда също така, че както "авторския", така и "каноничен" вариант
на метода на най-бързото качване яко ще се издъни на този простичек пример: точката
на локалния максимум в която алгоритм ще се приземи силно зависи от точката на старта
му. Ако се стартира от "цънтъра на тежестта" (синята точка), ще бъде върната
като оптимална една от дветте съседни червени точки, докато същинския оптимум очевидно
е най-лявата такава. Вижда се също така, че условието за единственост на оптималната
точка по никакъв начин не помага в намирането на точка от Z-околността
на оптималната, тъй че спокойно може да бъде махнато от формулировката на задачата.
Нормален безбъгов алгоритм чисто и просто би трябвало да връща произволна
точка, оптимизираща целевата функция със зададена точност epsilon
[7].
3. Разбира се, при многократно прилагане на subgradient или hill climbing алгоритм,
със случайно (и достатъчно голямо) множество от начални точки вместо една единствена,
шансовете за намиране на коректен локален максимум (т.е. максимален измежду всичките
локалните максимуми) се увеличават. Това става обаче за сметка на скоростта на алгоритма.
Т.е. Монте-Карло версия на алгоритма макар и по-коректна, нада ли ще се окаже достатъчно
ефективна.
6. Коментари към коментари.
[1] Aз
приложих модификация на част от този алгоритм за решаването на 6-та задача на миналогодишния
конкурс (Circles) която е дуална на разглежданата тук: там целевата функция f
беше дефинирана като f(P)=max{distance(P,Pi)} и се търсеше
нейния минимум,
което драстично упростяваше нещата, заради това че
f
е изпъкнала в този случай, и за нейно изчисление е било достатъчно да се използват
точки Pi само от изпъкналата обвивка на множеството от всички
точки. А изпъкналата обвивка беше до стотици пъти по-малка от множеството на всички
точки, заради спецификата на задачата. Е, загубих доста точки тогава заради използването
на скапания scanf() (мизерен максимален буфер на който -- 32К -- е останал, MS знае
защо, от епохата на DOS) вместо по-адекватен за големите файлове fread(). Всъщност
аз не използвах оригиналния сорс на Qhull, а написах своя код (само за 2D) въз основа
на авторското описание на Qhull
"The Quickhull Algorithm for Convex Hulls". Кода ми беше 2 пъти по-бърз от Qhull,
и аз бях много горд от това до момента, когато видях резултати и кода на Камен Добрев
за изчисляване на изпъкнала обвивка: той беше 15 до 30 пъти по-бърз от моя! Този
свръх бърз код исползваше до дупка специфични особености на задачата (целочислеността
на координатите на точките и относително малките размери на областта, в която те
се намират: квадрат 100000 на 100000), но не е изключено, че може да бъде обобщен
и за по-общ случай.
Както и да е, К.Добрев загуби тогава точки, защото негов brute force код за намиране
на оптималната точка беше много бавен в случая, когато изпъкналата обвивка бе голяма
(няколко хиляди точки). Впрочем имаше и един бъг: масив за точки от изпъкналата
обвивка се е оказал малък за един от тестовите файлове.
Друг интересен момент в тази задача беше, че за нея съществува и друго, "native",
решение, което не използва изпъкнали обвивки изобщо, намирайки директно вместо това
нещо, което може да се нарече "кръгова обвивка". Този алгоритъм, намерен от Мартин
Вълканов и Петър Петров, е много прост и бърз (те заеха първите 2 места тогава).
[2] Оригинална програма qvoronoi.exe е компилиран с много стара
версия на Borland C++ от 1995 г. Нейната рекомпилация с VC++6 би трябвало да ускори
програмата със около 20%.
[3] "Във много знание -- много печал", както е отбелязал Еклесиаст
на времето. Разбира се обратното твърдение също е вярно, въпреки законите на логиката.
Да речем, този, който знаеше ключовата дума "perfect match" (без дори да е чувал
преди това за Blossom IV или V ;-) е имал шанс да спечели доста екстра точки от
3-та задача.
[4] Тъй че твърдението от "авторския" коментар че външната оптимална
точка "...ще е или някой от върховете на многоъгълника или пресечна точка на контура
със симетрала на страна на многоъгълника" не е вярно, според мен, в общия
случай. А твърдението за O(N)-сложност на задачата при исползване на
алгоритма на R.Klein и A.Lingas за исчисляване на ограничени диаграми на Вороной
-- ако и е вярно, то поне не е толкова очевидно -- поне за мен.
Коментар на журито: Цитатът по-горе е грешен. Нашият
коментар казва "В случай, че търсената точка е извън многоъгълника, не е трудно
да се докаже, че това ще бъде точка, лежаща на страна на правоъгълника и
това ще е или някои от върховете му или пресечна точка на контура със симетрала
на страна на многоъгълника."
[5] Пример на един такъв лош случай ("змия"):
Тук N==17 само, просто за да се побере картинката в браузера. При N==1000000
точната версия на MaxPerim() би се издънила, докато евристичната би трябвало (ако
няма бъгове) да се справи много бързо.
[6] Току-що открих и тест-убиец на scaling алгоритм ("двe змии"
при N==34):
При N==1000000 програмата ми заглъхва. Предполагам че
причина за това дълго замисляне е
един цикл за попълване на масив от "разредените точки" в началото на MaxCircle(...);
този цикл пробягва върхове на многоъгълника и се изиква толкова пъти, колкото възела
има дървото на перспективните окръжности. Тъй като броя на възлите в този пример
е от порядъка 2*N, получаваме за този лош случай времева оценка О(N^2).
Какво може да се направи, за да се избегне многократно пробягване на този цикл?
Първото хрумване е: да се съберат всички локални масиви от разредените точки
(масив Pi[] в кода на MaxCircle(...)) в един глобален
тримерен масив Pi[depth][circle][index]; Тогава Pi[depth][][]
ще се попълва само веднъж, при достигането на дълбочината depth на
рекурсията.
Обаче това само по себе си не оправя нештата; трябва оше и да се измисли начина
за "обрязване" на вътрешен цикл в (псевдо)кода
for all(point)
for all(circle)
Add point to Pi[depth][circle];
Аз не знам в момента, дали такова "обрязване" (да речем, един филтър преди
"Add point... ", прекъсващ вътрешния цикъл) може да се направи. Но, както
се вижда от рисунката, в даден конкретен тест всеки един връх на многоъгълника ще
участва най-много само в две "съседни" окръжности от едно ниво, и интуитивно е ясно,
че и в общия случай броя на окръжности от едно ниво, споделящи всеки един конкретен
връх от многоъгълника е "малко", тъй че грехота е да се пробягва цикл по circle
от начало до край. Надявам се (след 15 април, естествено) да се върна към целия
код, да го поизчистя от бъгове и да ускоря, ако е възможно: задачата е една от тези,
с които е интересно да се занимава и извън контекста на конкурса.
[7] Не че моя собствен алгоритм е bug free <:((. Въпреки че
му оправих едноредов бъг, заради който загубих 2 точки, тъй че сега той се вмества
в прокрустово ложе Z=1.001 в 8-ми тест, все оше се намира на прекалено
голямо разстояние (0.53) от оптималната точка. Тъй като не използвах никъде в кода
този параметър и провеждах всички изчисления с максимална възможна точност, значи
има и още бъгове в моя код.
|