


 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
         |
 |
| Задача 6 - ОБИР НА БАНКА - Анализ |
|
И шестата (последна) задача от задочната част на Конкурса не беше
никак лесна (включително и за журито). Очевидно е, че задачата може да се раздели
на две части - намиране на всички мв-палиндроми и избиране на средния от тях при
лексикографска наредба. Да означим с S=S1 S2… SN
зададения текст. Нека първо разгледаме един директен подход за решаване на задачата.
Директното намиране на нечетните мв-палиндроми може да стане по
следния начин. За всяка буква Si на зададения текст, без крайните две, опитваме
да разширим тази буква до нечетен палиндром, т.е. за k=1,2,… проверяваме дали Si-k
е равна на Si+k. При първото несъвпадение прекратяваме проверките, тъй като е намерен
нечетен мв-палиндром (според условието една буква не образува палиндром). Аналогично
(започвайки от всяка двойка съседни еднакви букви) намираме всички четни мв-палиндроми.
За пестене на памет и удобство всеки намерен мв-палиндром можем да запомним с началото
и края му в текста (или с началото и дължината му). Очевидно сложността на този
алгоритъм в най-лошия случай е O(N 2) (например, ако текстът е
съставен само от една и съща буква).
За решението на втората част ще ни е необходимо да сравняваме мв-палиндроми.
Директният подход би бил да сравняваме двата мв-палиндрома буква по буква. Това
ни довежда до сложност O(N) в най-лошия случай на алгоритъма за сравняване
на палиндромите.
Нека намерените мв-палиндроми са M на брой. Директното намиране
на средния би било да сортираме всички палиндроми с O(M.logM) сравнения,
т.е при грубо сравняване за тази част ще получим алгоритъм със сложност O(N.M.logM).
В най-лошия случай M ще бъде O(N), но големината му в общия случай
зависи от конкретните входни данни.
Разбира се сортирането е ненужно за намиране на среден елемент
на множество. За намиране на К-тия пореден елемент на множество съществуват
много по-добри алгоритми. Алгоритъми със сложност O(M) сравнения могат да
се намерят във всяка сериозна книга по алгоритми (виж например Introduction to
Algorithms, T. Cormen, Ch. Leiserson, R. Rivest). Алгоритъмът със сложност O(M)
сравнения в най-лошия случай е труден за написване (и с голяма константа). За нашите
цели е напълно достатъчен много по-лесния за реализация алгоритъм със същата сложност,
но в средния случай (алгоритъмът е подобен на quick_sort). Така получаваме
решение на втората част със сложност O(N.M) в най-лошия случай или окончателно
за задачата O(N 2). За максималните стойности на параметрите на
задачата това е недостатъчно.
Сега ще се спрем на една сложна техника за решаване на задачи с
низове, която може да се използва за много по-бързо решаване не само на първата,
но и на втората част на задачата. Суфикс на низа S=S1 S2… SN
е всеки подниз на S, завършващ с буквата SN. Да означим с S*=S1
S2… SN$, където $ е знак, който не е измежду
буквите на S. Суфиксно дърво Т на низа S е кореново дърво с N+1
листа, ребрата на което са надписани със поднизове на S*, така че:
За по-бързо решение на втората част на задачата ще използваме също НОП. Нека d = НОП(LX,LY), където LX е листът в Т, съответстващ на суфикса, на който X е префикс; аналогично за LY. Да дефинираме функцията Less(X,Y) с аргументи мв-палиндромите X и Y, с дължини dX и dY, която връща стойност истина, ако X е лексикографски преди Y и неистина - в противен случай:
Като DFS(v) ни дава номера на v при preorder-обхождането на T в дълбочина, при което наследниците на текущия връх се обхождат в ред съответстващ на лексикографската наредба на изходящите ребра. Да отбележим само, че DFS номерирането е част от работата на алгоритъма на Schieber и Vishkin и не изисква допълнително време. Така сравняването на два мв-палиндрома става за константно време и втората част на задачата се реализира със сложност O(M).По този начин получаваме за цялата задача алгоритъм със сложност O(N+M)=О(N). Контстантите на този алгоритъм, разбира се, не са малки, но той може да се реализира за разумно време (3-4 дни) и е много ефективен. И все пак имаме участник, които без да се задълбочава в споменатите по-горе теории е успял да напише решение, което е много по-добро от решенията на останалите участници. Случайно или не, това е победителят от първия кръг от задочната част на Конкурса - Камен Добрев. Решението, според автора, използва техниката “Разделяй и владей” и описанието му може да се намери тук. |
Анализи на решения изпратени от участници: |
|
|
|
|
За въпроси можете да ни пишете на адрес: konkurs@musala.com.
Copyright 2000-2010 by Musala Soft Ltd. All rights reserved.
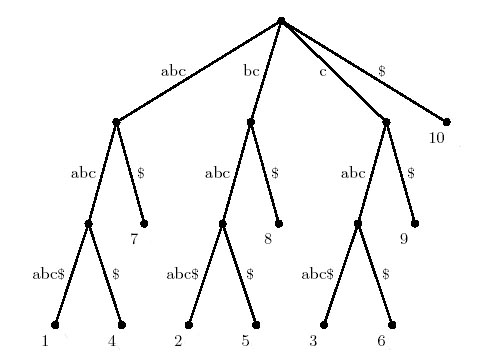 Макар и трудно построяването на суфиксно дърво на зададен низ може
да се направи със сложност O(N).
На
Макар и трудно построяването на суфиксно дърво на зададен низ може
да се направи със сложност O(N).
На