До скоро състезателното програмиране по-скоро избягваше т.н. NP-пълни задачи. Това са широк клас от интересни за практиката задачи (и съответно техните не по-лесни оптимизационни версии), за които не са известни “добри” (полиномиални) алгоритми. За намирането на точно решение на такава задача обикновено се прилага някаква форма на пълно изчерпване (най-често различни форми на алгоритмичната техника backtracking). Дори, когато алгоритъмът с пълно изчерпване за решаване на такава задача е допълнен с различни “хитрости” (оптимизации), които ускоряват работата му, времето за намиране на точно решение, при големи размери на входа, е неразумно голямо. Ето защо, вместо тотален отказ да се решават такива задачи на състезания по програмиране, се предпочете да се допускат неточни (неоптимални) решения и да се класират състезателите в зависимост от качеството на получения резултат.

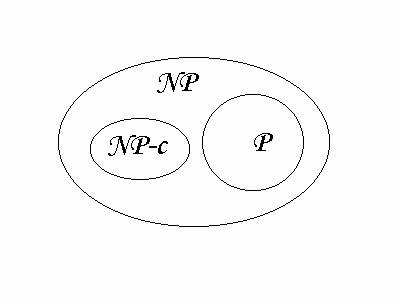
Тъй като съществува погрешното разбиране, че всяка алгоритмически “трудна” задача е NP-пълна, нека малко по-точно определим този клас. Да означим с P (виж Фигурата) множеството от задачи, за които съществува алгоритъм със сложност, изразявана с полином от размера n на входните данни. Повечето задачи от нашия Конкурс са били представители на този клас и ние сме се старали всеки път да посочваме съответния полином. Класът P е доста ограничен и извън него остават твърде много “трудни” задачи, които не са еднородни от гледна точка на сложността им. За се отдели от тях разумно множество, се въвежда класът NP (името на който се разшифрова неправилно като “не полиномиални”, защото всяка задача извън P е не полиномиална). Една неоптимизационна задача се включва в NP, ако съществува полиномиален алгоритъм, който по зададено “кандидат решение” проверява дали то е наистина решение на задачата. Затова NP се разшифрова като “недетерминирано полиномиални” или полиномиално “проверими” задачи.

За да се получи неоптимизационна версия на задачи за оптимизация, каквато беше четвъртата задача от Конкурса, се прилага елементарен трик. Вместо минималност (максималност) на решението се изисква то да не е по-голямо (по-малко) от някаква произволна константа С. Лесно се вижда, че задачата от конкурса е от NP. Алгоритъм, който проверява едно кандидат-решение, ще бъде със сложност O(n²), където n е броят на различните лаборатории. Ясно е, че задачите от Р са в NP, като полиномиален алгоритъм за проверка на решение на такава задача е алгоритъмът за решаване на задачата (или проста негова модификация). 

Исторически се е оказало, че за някои от задачите, класифицирани като NP, се намира след време полиномиален алгоритъм и те преминават в Р. За други задачи всички опити до момента се оказват безуспешни. Така се оформя генералният въпрос на теорията: “P=NP?”, отговор на който все още не съществува, а може и никога да не бъде намерен. Заради големият брой задачи от NP, за които все още не съществуват полиномиални алгоритми, може да се очаква, че отговорът е отрицателен. В опитите да се намери някаква теоретична трактовка на това предизвикателство, при предположението “P¹NP”, в NP се дефинира класът NP-c от т.н. NP-пълни задачи. Една задача p от NP е NP-пълна, ако съществува полиномиален алгоритъм за “свеждането” на всяка друга задача от NP към p. Свеждане означава трансформирането на входните данни на свежданата задача до входни данни на p и обратно, преобразуване на резултата на p в резултат на свежданата задача.

Полиномиалното свеждане на NP-пълна задача към някоя задача от NP доказва NP-пълнотата на последната. Всяко такова свеждане обикновено е нетривиален математически резултат. Истинското предизвикателство е било намирането на първата NP-пълна задача. През 1971 т. S. A. Cook доказва NP-пълнотата на следната задача: “Дадена е булева функция в конюнктивна нормална форма. Съществува ли вектор от стойности на променливите, за който функцията има стойност 1?” След доказването на този фундаментален резултат, чрез полиномиално свеждане е доказана NP-пълнотата на стотици интересни задачи, една от които е четвъртата задача от нашия Конкурс.

Какви са възможностите за намиране на добри субоптимални решения на NP-пълни задачи? На първо място ще споменем алгоритмичната техника наречена “лакома” (greedy). Лакомите алгоритми обикновено са много бързи, защото те не правят дълбок анализ на данните. С малки изключения (например известните алгоритми на Дейкстра, Прим, Крускал и др.) те не са в състояние да намерят оптималното решение в общия случай и все пак, понякога е много трудно да се построи тестов пример, който да “опровергае” добре направен лаком алгоритъм.

Ето един естествен лаком алгоритъм за решаване на нашата задача. Нека лабораториите са подредени по някакъв начин. Да обявим първата лаборатория за база. За всяка от останалите, по реда в който са зададени, да проверим кое ще излезе по евтино – да я обявим за база или да я свържем към най-близката от вече избраните бази. Сложността на този лаком алгоритъм е O(n²). Очевидно успехът му ще зависи от предварителното подреждане на лабораториите. Затова за подобряване резултата на работата му може да се приложи т.н. рандомизация. Т.е. да се опитат няколко (колкото времето позволява) различни случайни подреждания на лабораториите и да се избере това, което дава най-ниска цена. В много задачи най-добър резултат с лаком алгоритъм може да се получи при систематично подреждане (сортиране) на обектите по някакъв критерий.

Още един лаком подход ни беше подсказан от колеги, интересуващи се от конкурса. Да добавим един нов връх в пълния граф от връзки между лабораториите и да го свържем с всяка лаборатория с цената на оборудването й като база. Да построим минимално покриващо дърво с корен новодобавеният връх. Да изберем за бази тези от лабораториите, които са синове на корена. Всеки връх, който не е база и не е син на база в полученото дърво да преместим под най-близката до него база. В края на краищата не е изключено да се опита и директна атака като се разгледат всички подмножества от 1, 2, 3, и т.н. бази, докато времето позволява.

В теоретичен план е интересен т.н. апроксимационен подход. Той се състои в търсенето на достатъчно бърз алгоритъм за решаване на задачата p, който освен това гарантира получаването на резултат не по-лош от C.opt(p), където с opt (p) сме означили оптималното решение на задачата, а положителната константа С наричаме апроксимационна константа. Един от първите апроксимационни алгоритми за нашата задача, създаден от M. Charikar и S. Guha e с апроксимационна константа 1.728, базиран е на техниката на линейното програмиране и слажността му е много висока. По късно същите автори създадоха апроксимационен алгоритъм със сложност  O(n³) и константа 1.853. През 2001г. M. Mahdian, E. Markakis, A. Saberi и V.V. Vazirani предлагат апроксимационен алгоритъм със сложност O(n²log n) и константа 1.861. По-нов резултат в тази насока е на K. Jain, M. Mahdian и A. Saberi, които през 2002г. построиха алгоритъм със сложност O(n³), но с  константа 1.61. Този алгоритъм е подобрение на алгоритъма на M. Mahdian, E. Markakis, A. Saberi и V.V. Vazirani.

Ще представим накратко идеята на апроксимационния алгоритъм на K. Jain, M. Mahdian и A. Sberi, коxто по същество е лаком алгоритъм, базиран на техниката на линейното програмиране. Да означим с r_ij разстоянието между i-тата и j-тата лаборатория. Алгоритъмът работи във времето t и прилича на нещо като пазар. Когато една лаборатория не е избрана за база от алгопритъма, ще я наричаме просто лаборатория, а в противен случай – база.

1. Нека t=0, никоя от лабороториите не е избрана за база и съответно никоя не е свързана към база. За всяка лаборатория се определя бюджет B_j, който в началото  е нулев.

2. В определен момент на времето t всяка лаборатория j, предлага на  всяка друга лаборатория i част от бюджета си: p_ij = max(B_j - r_ij), ако j не е свързана до момента с база или p_ij = max(r_kj - r_ij), ако е свързана с базата k.

3. Докато има несвързана лаборатория:

Увеличаваме последователно времето t с единица, за всяка несвързана лаборатория j променяме B_j = t, докато се случи някое от следните 2 събития (ако на някоя стъпка и двете се случат, обработката им може да стане в произволен ред):

3.1. За някоя лаборатория сумата от направените предложения от други лаборатории става равна на цената за оборудването й като база. Тогава съответната лаборатория се обявява за база. Предложената част от бюджета  p_ij се нарича принос на j към i и този принос не може да се намалява от следващите стъпки на алгоритъма.

2.2. За някоя несвързана лаборатория j и за някоя база i бюджетът на j е равен на цената за свързване на  j към i. В такъв случай свързваме j към i, като p_ij=0.

            Малко по-късно M.Mahdin, Y.Ye и J.Zhang направиха алгоритъм с константа 1.52, съчетавайки алгоритъма на K. Jain, M. Mahdian и A. Saberi с този на Charikar, Guha и Khuller. Повече информация можете да намерите на “http://www-math.mit.edu/~mahdian/pub.html”.

 

И наистина апроксимационните алгоритми са добри – участниците заели второ и трето място използват гореспоменатите алгоритми с константи 1.52 и 1.61. Обаче апроксимациите най-често дават информация само за най-лошия случай, но не и как ще работи алгоритъмът в средния случай. Пробвайки различни подходи за решение (включително и апроксимациониите), победителят в този кръг Илиян Илиев е предпочел да се спре на следното решение: “избира се произволно решение, което след това се подобрява; на всяка стъпка се прави смяна - някоя лаборатория-не-база става база или лаборатория-база престава да бъде база, като след такава промяна за определен брой стъпки с тази лаборатория не може да се прави смяна; това се прави докато имаме време и докато сме намерили подобрение на решението за даден брой последни стъпки; разбира се, няма гаранция че това решение ще намери отговор близък до оптималния, но на практика работи добре”. Последното твърдение се доказа и от резултатите.