


 |
 |
 |
 |
 |
 |
 |
 |
         |
 |
 |
 |
Задача 1 от брой 10/2003 - МОЛЕКУЛИ - Анализ
Алгоритмите за решаване на различни задачи върху низове са сред най-често използваните. С разпространението на Интернет технологиите, както и приложенията на компютрите в такава модерна дисциплина като генетиката, тяхното значение нарасна извънредно много. При това дължините на данните в реални задачи от този тип (текстове публикувани в Интернет или сложни биологични образования, представени с низове) се измерват обикновено с милиони или даже милиарди байтове. Затова интерес представляват не просто алгоритми за работа с низове, а алгоритми с много висока скорост. Много често в реалния живот може да възникне задача, за която в литературата не може да се намери подходящо решение и на програмистите се налага да модифицират някоя от известните техники. За първа конкурсна задача през тази година избрахме задача от подобен вид.
Една от най-популярните задачи върху низове е задачата за търсене на зададен низ P (наричан шаблон) в друг зададен низ T (наричан текст). Счита се за естествено, че дължината N на текста значително надвишава дължината K на шаблона. В литературата са добре известни алгоритмите на Боер-Мур и Кнут-Морис-Прат (КМП) за решаване на тази задача. Познаването на алгоритъма КМП би улеснило много разбирането на анализа на задачата. Напоследък, с появата на книгата Algorithms on Strings, Trees, and Sequences на Dan Gusfield (на нашия пазар може да се намери руския й превод Строки, деревья и последовательности в алгоритмах) стана популярен и естественият и лесен за запомняне и затова по-използваем в състезания по програмиране Z-алгоритъм. Горещо препоръчваме на уважаемите читатели тази книга, още повече, че настоящият анализ се основава на материала изложен в нея.
В основата на нашата задача е залегнало едно естествено обобщение на споменатата по-горе задача за търсене на шаблон P в текст T. Вместо един шаблон е зададено множество от шаблони {P1, P1,…, PM}, което наричаме речник и се търсят всички срещания на всеки от шаблоните в текста. В този случай с D ще означаваме сумата от дължините на всички шаблони. Задачата е допълнително усложнена, като се търси най-късият подниз от текста съставен от два шаблона, разделени с непразен низ, който не е шаблон.
Да започнем с първата част на задачата. Ще разгледаме алгоритъма на Ахо-Корасик (АК), който в някакъв смисъл обобщава алгоритъма КМП. Един наивен алгоритъм, за установи дали P се среща в T от позиция L, би започнал да сравнява последователно T[L] с P[1], T[L+1] с P[2], и т.н. докато установи срещане на P в T или несрещане, след което да направи същото от позиция L+1 и т.н., а сложността му в най-лошия случай ще бъде O(N.K). За да избегне наивното сравняване, КМП извършва предварителна обработка (препроцесинг) на шаблона, която може да му позволи, при първо несъвпадение, да продължи търсенето не от позиция L+1, а от някоя позиция по-голяма от L+1, ускорявайки по този начин работата.
Подобна идея използва и АК, като засега ще предполагаме, че никой шаблон не е начало на друг шаблон. За целта първо се построява дърво на шаблоните, както е показано на Фиг. 1 за речника {da,ab,cabc,cabda}. Важно свойство на това дърво е, че за всеки шаблон (а така също за всяко начало на шаблон) имаме единствен път от корена до някой от върховете на дървото, така че последователността от буквите по този път съвпада с шаблона. Върхът, който е край на пътя обозначаваме с поредния номер на шаблона в речника. С помощта на дървото на шаблоните можем да реализираме наивен алгоритъм за обобщената задача подобен на описания по-горе. Аналог на препроцесинга на
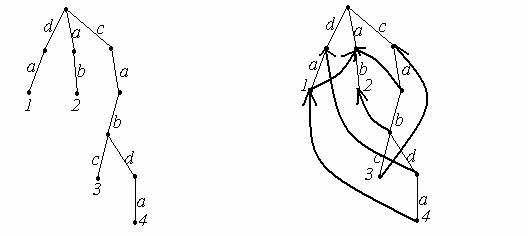
фиг.1 фиг.2
КМП е следното разширение на дървото на шаблоните. Да означим с av думата съответна на върха v, с l(v) – дължината на най-дългия край (суфикс) на av, който е начало (префикс) на шаблон, с S(v) – съответното начало, а с nv – върхът до който се стига от корена на дървото с думата S(v). Ако l(v)=0, тогава S(v) е празната дума и nv е коренът на дървото. Да свържем всеки връх v, за който l(v)>0 със съответния му nv, посредством ребро, ориентирано от v към nv. За останалите върхове ориентираните ребра сочат корена и не е нужно да ги показваме явно. Резултатът от тази процедура за дървото от Фиг.1 е показан на Фиг.2. С използване на така полученото разширение получаваме следния алгоритъм (предварителна версия на АК за случая, когато никой шаблон не е начало на друг шаблон):
L=1;C=1;V=корена;
do
{ while (има ребро (V,V’) надписано с T[C])
{if (V’ е надписан с i)
Pi започва от T[L];
V=V’;C++;
}
L=C-l(V);V=nV;
} while(C<=N);
Идеята на този алгоритъм, подобно на КМП е, че когато сравняването завърши с неуспех във върха V, не нужно да се повтаря успешно преминалото сравняване на S(V), а направо трябва да се продължи от върха nV, в който свършва пътят от корена, надписан с S(V). Очевидно сложността му е О(N), защото за всяка буква на T извършва не повече от константен брой операции. За работата му е необходимо да можем за всеки връх v да намираме ефективно съответния му nv.
Ако V e корена R или някой негов син, тогава очевидно nV=R. Затова да допуснем, че вече сме намерили nV за всеки връх V, който се намира на разстояние £H от корена. Следната процедура изпълняваме за всеки връх V намиращ се на разстояние H+1 от корена:
V’=бащата на V;x=буквата на (V’,V);W=nV’;
while (няма ребро (W,W’) надписано с x и W¹R)
W=nW;
if (реброто (W,W’) е надписано с x) nV=W’;
else nV=R;
Действително, ако в началото съществува ребро излизащо от W=nV’, надписано с x, то очевидно краят му е точно nV. Ако такова ребро няма, то най-дългия край на низa, завършващ във V и е начало на шаблон, трябва да се търси в nW. Ако и там няма подходящо ребро, се продължава по същия начин, докато се намери такова ребро или се достигне до корена. За доказателството на правилността на процедурата е много важно да се отбележи, че за всеки връх V, съответният му nV е на по-малко разстояние от корена отколкото самия V. Не е много лесно да се види, че тази процедура е със сложност O(K), където К е общата дължина на всички шаблони.
Сега да се върнем към действителната ситуация, която не изключва един шаблон да е начало на друг шаблон. Да наречем ориентираните ребра в разширеното дърво на шаблоните връзки. Път, съставен от връзки, започващ във върха V и завършващ във връх W, първият по пътя, който е надписан с номер на шаблон ще наричаме външна връзка. Външните връзки са ефективен начин за придвижване по връзките в дървото за достигане на номериран връх. В сила е следното твърдение: по време на работата на алгоритъма може да се достигне връх V, от който излиза път от външни връзки към връх надписан с i тогава и само тогава, когато шаблонът Pi се среща в T и краят му е в текущата позиция С. Тази теорема ни дава следната окончателна форма на АК:
C=1;V=корена;
do
{ while (има ребро (V,V’) надписано с T[C])
{if (V’ е надписан с i или има път от
външни връзки от V’ до V” връх с номер i)
Pi завършва в T[C];
V=V’;C++;
}
V=nV;
} while(C<=N);
Сложността на общата версия на алгоритъма АК е O(К+N+Z), където Z е броят на срещанията на шаблони в текста.
Алгоритъмът АК е отлично средство за решаване на първия етап на задачата, но в частни случаи получените от него резултати са много обемисти и втората фаза от решението на задачата, нито може да работи за прилично време нито да си позволи да съхранява и използва всички срещания на шаблони в текста. Лош частен случай би бил речник, в който всички думи са съставени от една и съща буква и текстът – също от тази буква. В този случай практически всяка буква от текста е край на всички шаблони, т.е. имаме Z = O(NM) срещания на шаблони и един наивен алгоритъм за втората част на задачата (да се сравнява всяко срещане със всяко друго за да се намери точния оптимум) е обречен на неуспех.
И така за втората фаза най-разумно е да се избере достатъчно бърз и разумен greedy подход. Предлагаме на вниманието на читателите две такива идеи.
Нека най-късият шаблон, който завършва в i-тата позиция на текста започва в позиция left(i). Очевидно е, че ако този шаблон участва в решение като лява част, то всеки друг шаблон завършващ в i ще участва в по-лошо решение. Следователно можем да си спестим разглеждането на другите шаблони, завършващи в i. Лесно може да се модифицира АК така, че път от външни връзки от V до номериран връх W да бъде заменян с единична външна връзка. Ако това се прилага рекурсивно, в края на работата външната връзка на V ще сочи към номериран връх връх V’ такъв, че αV’ е най-късия край на αV който съответства на път от корена до номериран връх. Тогава left(i) си изчислява, за всички i, от АК със сложност O(N) след препроцесинг със сложност O(K).
Нека шаблонът, който се среща в текста (започва) на или след (i+1)-ва позиция и краят му е най-близко до i-тата позицията завършва в right(i). Ако се окаже че i+1<left(right(i)) то T[i+1..left(right(i))-1] не е шаблон и тройката (left(i), i+1, left(right(i))) е кандидат за решение. Остава да се избере най-доброто от тези кандидати за решение. Сложността на тази стъпка ще бъде O(N). Тази greedy процедура си има своите дефекти и един контрапример е споменатият по-горе случай, когато и шаблоните и текста са съставени само с една буква, при това шаблоните са с дължини 1,2,3,.... Тогава процедурата не намира решение. Това се дължи на “слабостта” му да работи лошо, когато "трудно" (не често) се намира подниз, който не е шаблон.
Нека за всяка позиция от текста j означим с end[j] дължината на най-късия шаблон завършващ в позция j, а с beg[j] дължината на най-късия шаблон започващ в позиция j. След като алгоритъма на АК намира всички шаблони завършваща в произволна позиця i, то той намира и всички не-шаблони завършващи в позиция i (това са всички познизове на текста с начала 1, 2, ... i и край i без тези от тях които са шаблони). Тогава за всяка позиция i от текста можем да разгледаме няколко нешаблона, като ако шаблон е с начало j ще имаме кандидат за решение подниза от позиция j-end[j-1] до i+beg[i+1] който ще се рабива на три последователни част с начала съответно j-end[j-1], j, i+1. Разбира се end[j-1] и beg[i+1] трябва да са дефинирани в съответните си стойности - затова този алгоритъм няма да работи добре когато щаблоните не се срещат често в текста. Да се разглеждат всички не-шаблони за дадена позиция i би довело до абсолютно вярно решение, но работещо със сложност O(N2). Ето защо е разумно да се разглеждат само някои от шаблоните - на пример, може да се разглеждат няколко "дълги" не-шаблони (по-дълги от най-дългия шаблон завършащ в позиция i) и няколко "къси" (по-къси от най-късия шаблон завърващ в позиция i).
Така използвайки алгоритъма на АК и тези два greedy подхода можем да намерим добър отговор (не винаги оптимален) със сложност O(N) след препроцесинг със сложност O(K).
За въпроси можете да ни пишете на адрес: konkurs@musala.com.
Copyright 2000-2010 by Musala Soft Ltd. All rights reserved.