Конкурсната задача под номер 3 е представител на един широк кръг задачи в графи, наричани Задачи за намиране на оптимален път в граф. Тези задачи се поставят за графи (ориентирани или не), по ребрата на които е дефинирана функция c, наричана дължина (тегло, цена и т.н. ) на реброто. За реброто от върха i до върха j да означим стойността на тази функция с сij. По някакъв естествен начин се дефинира c(L(i,j)) - дължина (тегло, цена и т.н. ) на произволен път L(i,j)от върха i до върха j като функция на дължините на участващите в него ребра. Целта на задачата е да се намерят пътища с оптимална дължина от зададен връх до друг зададен връх, от зададен връх до всички останали върхове или от всеки връх до всеки от останалите. Оптималността се определя по някакъв критерий opt, пресмятан върху дължината на пътя.
Изключително добри алгоритми за задачите от горния тип съществуват, когато за задачата е в сила следното свойство:
Opt(c(L(i,j))= Opt(c(L(i,k))* Opt(c(L(k,j))
където k е произволен връх от пътя L(i,k), а * е операция, зависеща от спецификата на задачата. В такъв случай алгоритмите обикновено се състоят от повтаряне на всяка стъпка на операция от следния вид
c(i,j)= Opt{c(i,j), c(i,k)* c(k,j)}
наричана релаксация, която преизчислява дължината c(i,j) на намерения до момента оптимален път, като го сравнява с дължината на намерения до момента оптимален път, минаващ през върха k.
Типични примери за такива алгоритми са Алгоритъмът на Дейкстра (за намиране на най-къс път от зададен връх до всички останали) и Алгоритъмът на Флойд (за намиране на най-къс път от всеки връх до всички останали). В този случай дължината на път е сумата от дължините на ребрата критерият за оптималност е минимум, а операцията * е събиране.
Задачата за намиране на път с най-висока надеждност, която се получава от конкурсната задача при еднаква пропускливост на всички ребра, е задача от такъв тип. За нея релаксацията е P(i,j)= max{P(i,j), P(i,k).P(k,j)}. От такъв тип е и задачата за намиране на път с най-висока пропускливост, която се получава от конкурсната задача при еднаква надеждност на всички ребра. За нея пък релаксацията е Q(i,j)= max[Q(i,j),min{Q(i,k),Q(k,j)}].
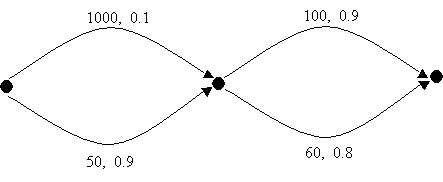
Конкурсната задача обаче, получена от смесването на двете споменати задачи и наричана задача за пътя с максимална редуцирана пропускливост, не е от същия тип. Например на фигурата по-долу комбинацията от двете ребра с максимална редуцирана пропускливост има цена 10, докато комбинацията на другите две ребра дава път с максимална редуцирана пропускливост 36.

Ще опишем идеята на итерационен алгоритъм решаващ задачата за намиране пътя с максимална редуцирана пропускливост (за краткост ще го наричаме оптимален) от някакъв начален връх v до някакъв краен връх w. Нека G0 (V,E0) е зададеният граф. Да намерим в G0 (V,E0) пътят с максимална пропускливост от v до w и нека Q е неговата пропускливост. Да намерим в G0 (V,E0) и запомним пътя L0 от v до w с максимална надеждност и нека Q0 е пропускливостта на този път. И в двата случая използваме алгоритмите, които дискутирахме вече. Да образуваме множеството E1 като премахнем от E0 всички ребра с пропускливост по-малка или равна на Q0. Нека графът G1(V,E1) е свързан, т.е. в него има път между всеки два върха. Ще покажем, че или L0 е оптимален или графът G1(V,E1) съдържа оптимален път от v до w. Ако L0 не е оптимален, тогава за оптималния път имаме, че надеждността му не може да надхвърля тази на L0 (поради това, че L0 е с максимална надеждност), а редуцираната му пропускливост трябва да бъде по-голяма от тази на L0 и следователно оптималният път не може да съдържа ребро с пропускливост по-малка или равна на Q0 и значи всички ребра на оптималния път са в G1(V,E1). Нека пътят от v до w в G1(V,E1) с максимална надеждност е L1 и неговата приведена пропускливост е по-добра от тази на L0. Тогава L0 не е оптимален. Да запомним L1 като най-добрия намерен до момента, вместо L0, и да повторим направеното по-горе разсъждение за графа G1(V,E1) и пътя L1. Така построявяме граф G2(V,E2), който трябва да съдържа оптималния път, ако L1 не е оптимален и т.н.
Процесът трябва да спре ако графът Gr(V,Er) се окаже несвързан (т.е в него няма никакъв път от v до w) или тогава когато редуцираната пропускливост на най-добрия намерен до момента път се окаже по-голяма от произведението Q.P(Lr), където Q беше максималната пропускливост на път от v до w в началния граф, а P(Lr) максималната надеждност на път от v до w в текущия граф Gr(V,Er). Ясно е, че тъй като величината P(Lr) намалява със всяка стъпка на алгоритъма, а надеждността на е може да бъде по-голяма от Q, следващите стъпки на алгоритъма няма да дадат по-добър от намерения до момента път.