Задача 4 - ТРЪБОПРОВОД - Анализ За решението на четвъртата конкурсна задача са важни само точките с цели координати. Затова да направим едно традиционно преобразуване - вместо координатна система, да разгледаме безкрайна мрежа от клетки, в която на всяка точка с цели координати е съпоставена съответна клетка. Ако точка със зададени координати е част от преградна стена, то съответната й клетка ще е запълнена. В противен случай клетката ще бъде празна (вж. фигура 1). 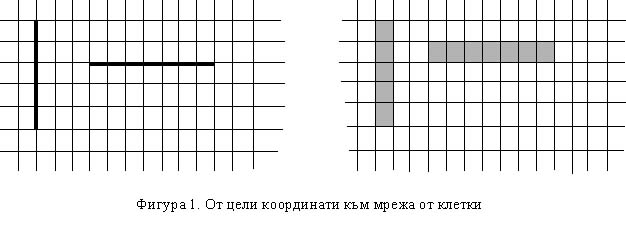За решението на задачата са важни не дължините на отделните части от тръбопровода, а броят на колената. Затова първо ще трансформираме изложбеното пространство до еквивалентно на него с по-малки размери, за което след това по-лесно ще намерим тръбопровод с минимален брой колена. Идеята на трансформацията е следната. Да разгледаме две преградни стени успоредни на ординатната ос (т.е. във всяка от тях клетките имат равни х-координати). Ако стените са долепени една до друга (разликата в х-координатите им е 1), очевидно между тях не може да се построи тръбопровод. Ако не са долепени (разликата в x-координатите им е 2 или повече), тогава очевидно между тях може да се построи тръбопровод. Частта от оптимален по брой колена тръбопровод, преминаваща между две успоредни стени, винаги е успоредна на стените. Затова, разстоянието между такива две стени може да бъде сведено до 2, ако то е по-голямо. При стените успоредни на абсцисата нещата са аналогични. За трансформиране на изложбеното пространство (както по х- така и по у- координати) прилагаме следната процедура: сортираме точките, които са краища на преградните стени, включително началото и края на тръбопровода, по съответната координатата; на координатата на първата точка съпоставяме 2 (да не забравяме че за да бъде оптимален тръбопроводът може да се наложи да “заобиколи” всички стени отляво/отдолу); нека координата на последната обработена точка е q, а на текущата е r. Ако на координатата на последната обработена точка сме съпоставили q’, то на текущата ще съпоставим r’, като ако r-q=0, то r’= q’, ако r-q = 1, то r’ = q’+1, а ако r-q >= 2, то r’ = q’+2; нека u е стойността съпоставена на последната от сортираните x-координати, а v е стойността съпоставена на последната от сортираните y-координати. Така трансформирахме изложбеното пространство до правоъгълника P={(x,y) | 1<= x<=u+1, 1<=y<=v+1}. 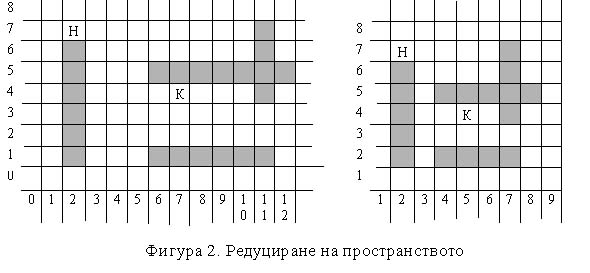Фигура 2 илюстрира описаната трансформация. При този начин на опростяване u,v <= 2*M, където M е броят на всички сортирани точки. Според условието N <= 100. Следователно M=2*N+2<=2*100+2 и u,v<=2*(2*100+2)=404 т.е. максималният интервал в който бихме могли да разглеждаме коя да е от двете координати е [1, 405]. Сведохме задачата за намиране на път от зададена клетка до друга зададена клетка в правоъгълна мрежа не по-голяма от 405x405, като пътят трябва да е с минимален брой завои (колена). Тази задача може да бъде решена с различни вариации на стандартните алгоритми за намиране на най-къс път в граф или обхождане в широчина. От всяка празна клетка на мрежата да направим два върха на граф - vh и vv (единият съответстващ на достигане на клетката с движение по хоризонтал, а другия - по вертикал). Двата върха vh и vv са свързани с ребро, теглото на което е 1. Всеки “хоризонтален” връх е свързан с хоризонталните върхове на съседните по хоризонтала празни клетки с ребро, теглото на което е 0. По същия начин всеки “вертикален” връх е свързан с вертикалните върхове на съседните по вертикала празни клетки с ребро, теглото на което е 0. Стандартният алгоритъм на Дейкстра в получения граф решава задачата. За целта в началото и двата върха, съответни на началната клетка на тръбопровода се обявяват за “обходени” с дължина на най-късия път равна на 0. Алгоритъмът прекратява работата, когато “обходи” някои от върховете съответни на крайната клетка на тръбопровода. Препоръчително е да се използва оптимизираната версия на Дейкстра алгоритъма, използваща Fibonacci heap, която ще доведе до O(K*logK +L), където К е броят на върховете, а L - броят на ребрата в графа. Понеже L e O(K), то сложността ще е O(K*log K).Интересно е, че в случая може да използваме алгоритъма за обхождане в широчина, за да намерим най-късите пътища в графа. Първо построяваме графа по описания по-горе начин, при който на всяка клетка съпоставяме два върха на графа. За получения граф трябва да се приложи модифицирано обхождане в широчина. Понеже имаме и ребра с тегла 0, нужна е една малка промяна спрямо класическия алгоритъм - при достигането на даден v връх със сума l на теглата на ребрата от пътя (дължина l), трябва да обработим и всички върхове, до които се стига от него само чрез ребра с тегла 0. Тези върхове също ще бъдат достигнати с дължина l. Така, първата стъпка ще бъде да се обработят всички върхове, до които се стига с дължина 0; после всички върхове, до които се стига с дължина 1 и т.н. Щом достигнем някой от върховете съответни на крайната клетка на тръбопровода, ще сме намерили тръбопровод с възможно най-малко колена. Сложността на обхождането в широчина е O(K+L), където К е броят на върховете, а L - броят на ребрата в графа. Понеже L e O(K), то сложността ще е O(K). Анализи на решения изпратени от участници: Камен Добрев

За въпроси можете да ни пишете на адрес: konkurs@musala.com.

Supported by Musala Soft Ltd.

Copyright 2000-2010 by Musala Soft Ltd. All rights reserved.