Musala Soft and PC Magazine Bulgaria

Конкурс по програмиране на Musala Soft и PC Magazine Bulgaria

Състезателна система

Коментари към 3-та задача
В.Молотков

1. Тривиална ли е задачата?.

Основната цел на тези мои коментари е да се покаже, че задачата не само не е тривиална, както твърди Иван Москов в своето 1-во писмо до журито, но реално е много по-сложна, отколкото би била, ако би се приела нейната, според доц. Красимир Манев, "по-добра" формулировка. Отчитайки факта, че става дума не само за пореден етап на конкурса на PC Magazine, но и финален (и единствен) етап на конкурса на БАССКОМ с доста солиден награден фонд, такава повишена сложност на задачата е, според мен, напълно оправдана. Дори това да не е била целта на журито, а се е получило неволно с избора на "по-лоши" ;-) правила за join и split. А това, че тя се е отклонила от семантиката на реални програмни системи, според мен, изобщо не е важно. Главното е, че се е получила интересна и трудна задача.

Тъй че аз не мога да се съглася с доц. Красимир Манев, който пише, вероятно под натиска на тази критика, която не е адекватна почти във всички свои пунктове, а в някои дори е смешна (вж. раздел 5.), че вариантът, избран от журито, е "дефектен".

Друг е въпросът, че на практика много малко от участниците, за моето голямо учудване, са могли да забележат парадоксалните и много красиви начини за точна оптимизация. Освен мен това са били Евтим Георгиев и Камен Добрев (доколкото може да се съди по сорс кодовете преглеждани по-диагонала). За съжаление адекватната реализация на тези парадоксални решения изисква много повече както кодиране така и дебъгване, отколкото рутинните методи на локалната оптимизация с различни варианти на greedy алгоритми. Да не говорим за времето необходимо за теоретично изследване и обобщаване на алгоритма до неговите естествени граници.

В същност за адекватното реализиране на оптимизацията трябва да се напишат, както ще бъде демонстрирано по-долу, няколко алгоритма от различно естество, само един от които е рутинен greedy алгоритм. Тези алгоритми (с различна времева сложност) се нареждат в един конвейер, който търси в дадена система "интересни" подсистеми, позволяващи точното оптимизиране. Само ако такъв интересен обект не бъде намерен, се включва greedy алгоритъм, който намира "почти" оптимално решение.

2. Кой е победителят?

Въпреки тези допълнителни трудности един от тримата състезатели, сетили се за такива алгоритми -- Евтим Георгиев -- би могъл да заеме 3-то място в турнира на БАССКОМ, ако програмите за тестване нямаха бъгове. А ако и формулата за изчисляване на точките не би била модифицирана с log в сравнение с обявената от самото жури в коментар 3 на сайта, то той би заел и 1-во място, а Камен Добрев -- 3-то (вж.раздел 4)! Ако това бе станало, аз вероятно не бих имал никакви стимули да си губя времето в писането на тези коментари, тъй като бих преживял много по-леко моето собствено поражение (заради един изключително тъп бъг): това че хубавите алгоритми победиха, макар и не в моята собствена реализация за мен е едно утешение -- не знам защо. Но стана това, което стана. Във всеки случай, за разлика от резултатите на първите тестове, които очевидно не могат да бъдат преразгледани (премиите са раздадени вече), аз смятам, че нищо не пречи да се коригират точките за вторите тестове по правилната формула:

точки за тест = (100/брой тестове)*(подобрение на баланса)/(максимално подобрение на баланса).

Очевидно няма друг начин да се интерпретират думите от 3-ти коментар към 2-ра задача на сайта:

"програмите ще получат брой точки, пропорционален на подобрението на баланса спрямо най-голямото подобрение на баланс от програма на участник."

A oткъде и защо е възникнала формулата с log:

точки за тест = (100/брой тестове)*log(1+подобрение на баланса)/log(1+максимално подобрение на баланса)

с която се изчисляваха на практика точките -- не ми е ясно. Този log намалява разликите в точките между тези на шампиона (в даден тест) и следващ го по резултат, което довежда до една "уравниловка". Разликата в подобренията може да бъде малка, но постигната с много по-голям труд при писането на код за точните алгоритми. А при логаритмуване тази малка разлика ще става много по-малка, тъй че този допълнителен вложен труд остава невъзнаграден.

3. Алгоритми.

3.1. Основен трик.

Нека в изходната система има подсистема от следния вид: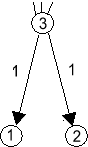

	или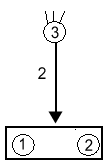
Фиг.0s		Фиг.0p

където неутралните модули 1 и 2 от Фиг.0s (съответно паралелният модул от Фиг.0p) са финални в смисъл, че не съществува нито една връзка излизащa от тях, и освен това има само една връзка към тях -- тази от модул 3. Модул 3 на тези фигури е неутрален, но може да бъде и сериен (в този случай просто отцепваме последния фрагмент от него за да получим подсистема от вида изобразен на Фиг.0). Освен това подсистемата от Фиг.0р със "split 1" се привежда към подсистема от Фиг.0s, тъй че по-нататък ще разглеждаме само случая на два неутрални финални паралелизуеми модула (т.е. такива, че могат да бъдат обединени в един паралелен модул с една операция join).

Също така ще дефинираме една важна операция BlowUp(i,j,n) състояща се от join(i,j), split(i) повторено n пъти (тук i и j е произволна двойка от неутрални паралелизуеми модула, такава че i<j). Защо тя е толкова важна може да се разбере, ако се погледне резултатът от прилагането на BlowUp(1,2,50) към подсистемата от Фиг.1s:

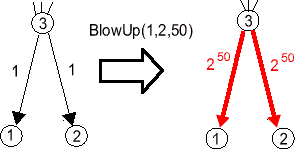Фиг.1

От Фиг.1 се вижда, че теглата на връзките 3-->1 и 3-->2 се раздуват (оттам името BlowUp), т.е. придобиват такива гигантски размери, които буквално издухват сумата от всички останали тегла на връзки в системата (както външни, така и вътрешни). Т.е., ако обединим модулите 1,2 и 3 (join(3,1),join(1,2)) в един сериен модул, след което разбием всички останали серийни и паралелни модули на модули с по 1 фрагмент, ще получим в резултат система с баланс, много близък до N/(N-2), тъй като частно S_m/S, а значи и целият втори член в дефиницията на баланса ще е много близък до нула. Лесно се вижда, че освен при системите с малки N (3 или 4), баланс по-малък от N/(N-2) не може да бъде постигнат (ако в началната система има поне две връзки, разбира се). Ние можем да се доближим до това шампионско решение на произволно малко разстояние, като вземем достатъчно голямо n в BlowUp(1,2,n). Ето защо е необходимо ограничаване на точността на измерване на баланса в задачата. При точност 6 знака след десетичната точка n=50 (в краен случай 100) е достатъчно във всички случаи. И няма да побърка тестващите програми в случай, че журито не е взело предпазни мерки :). Като една такава мярка е достатъчно всяко едно от теглата (както външно така и вътрешно) да се раздели на сумата от всички тегла всеки път, когато тази сума надхвърли някаква горна граница (да речем DBL_MAX/2): това действие очевидно няма да промени стойността на баланса. Самата програмата за оптимизация няма да се обърка дори и при n=1000000, защото ако програмата намери подсистема от типа изобразен на Фиг.0 (или по-сложни типове, разгледани долу), тя изобщо няма нужда да изчислява баланса, освен в режим на дебъгване, в който n може и да се намали :). А и самата операция BlowUp може да е чисто виртуална: няма нужда да се произвеждат каквито и да са операции над реална подсистема, достаточно е само да се запише в изходния файл съответната редици от операции.

Всичко това е добре, обаче какво ще правим в случая, че подсистеми от такъв тип в началната система няма? Например, нито една система от тестовете 1-11 не съдържаше такава хубава подсистема. По-нататък ще видим, че може да има и други хубави подсистеми, даващи същото гранично решение N/(N-2). И ако тестовете се генерират с генератор на случайни числа, то като че ли вероятността на присъствието на поне една хубава подсистема е близо до 1 при голямо N.

3.2. Още един трик.

Да предположим, че в изходната система съществуват два финални неутрални модула, които не са паралелизуеми, обаче се намират в една и съща компонента на свързаност на граф представящ системата. С други думи, съществува неориентиран път в графа, свързващ тези два модула. Тогава е валидно следното твърдение: съществува поредица от оператори join и split, след която тези два финални модула ще станат паралелизуеми. По-конкретно, след като бъде намерен съответният път между двата финални модула (да речем с алгоритма на Дийкстра) едно обхождане на този път прави това, което ни трябва. Няма да пиша псевдокод за това обхождане, а ще дам един конкретен пример, размишлявайки върху който, всеки може да напише съответния код и за общ случай (само че трябва и да го тества: един от бъговете в моята програма се криеше тъкмо в това обхождане :(( ).

Начално състояние:

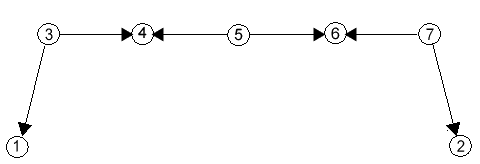Фиг.2a

1. След join(3,4),split(3):

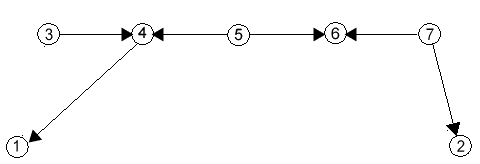Фиг.2b

2. След join(5,4):

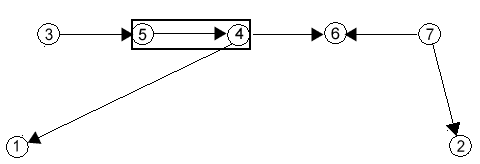Фиг.2c

3. След join(5,6),split(5),split(4):

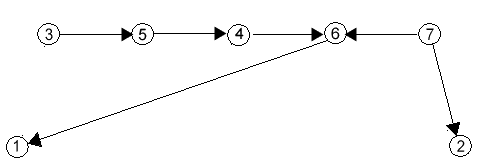Фиг.2d

4. Най-накрая, след join(7,6) ще получим:

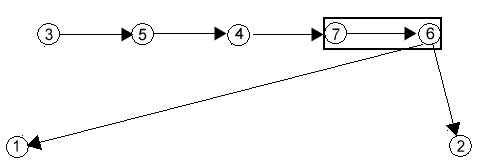Фиг.2e

И така, можем вече да приложим трик с BlowUp, за да получим шампионско решение с баланс почти равен на N/(N-2).

В горния пример междинните модули от пътя могат да бъдат от произволен тип. Ако някой от тях е паралелен, трябва просто да се отцепи от него един фрагмент. Тъкмо този фрагмент ще участва в операциите join и split вместо самия паралелен модул.

Времевата сложност на алгоритм за търсене на такова едно решение е равна на сложността на исползвания в него алгоритм за намиране на най-късия път, т.е. O(N+броя на линкове) ако се исползва алгоритм на Дийкстра с FIFO опашки. Които могат да се исползват тук вместо приоритетни: теглата на връзките при намирането на пътя за нас не са от значение, тъй че в алгоритъм на Дийкстра можем да ги смятаме всичкитете равни на 1, при което приоритетна опашка се изражда в FIFO и исчезва един log във времевата оценка на алгоритма. В тестовете на журито този алгоритм би успял само в един от тестовете (11-ти във версията на БАССКОМ или 10-ти в настощата).

3.3. По-сложни случаи.

Какво ще стане в случая, когато няма нито един финален паралелен модул, нито два финални серийни в една и съща компонента на свързаност на графа? Оказва се, че може да има и други подсистеми, които могат да произведат същия граничен баланс N/(N-2) като резултат на комбинация от подходящи операции върху тях. Те се подразделят на два класа: локални и нелокални. Локалните хубави подсистеми се характеризират с това, че ако намерим в дадена система само една такава подсистема, то са достатъчни операции само върху тази подсистема за оптимизирането. Докато за да се постигне същия резултат с нелокалните хубави подсистеми трябва да се намерят две такива подсистеми както и един неориентиран път между тях с някои специални свойства.

3.3.1. Локални подсистеми.

Това са подсистеми от следния вид:

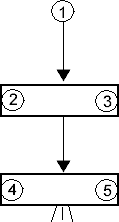	или		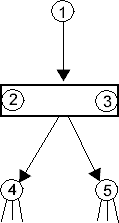или		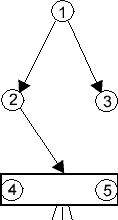или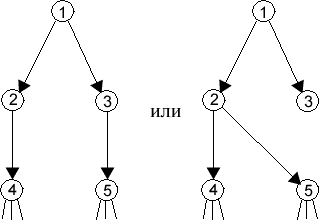
Фиг.3pp		Фиг.3ps		Фиг.3sp		Фиг.3ss

където неутралните модули 1, 4 и 5 могат да бъдат заменени и съсъ серийни, докато паралелните модули могат да съдържат и повече от два фрагмента. В последния случай преди да се пристъпи към оптимизацията трябва да се отцепи от всеки паралелен модул едно парче с 2 фрагмента. Едно важно ограничение за всяка една от тези локални подсистеми е: не трябва да има връзки от "долните" модули (4 или 5) към "средните" (2 или 3). Обратните линкове от 2 или 3 към 1, ако ги има, няма да попречат на оптимизацията.

Самият процес на оптимизацията може да бъде изобразен ето така:

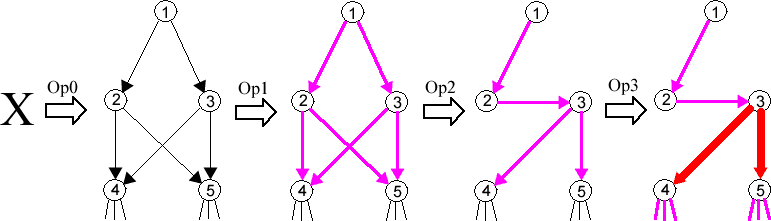
Фиг.4

където X може да е всяка една от системите изобразени на Фиг.3;
Op0 е очевидна комбинация от join/split (split(2), split(4) за Фиг.3pp, и т.н.).
Op1: BlowUp(2,3,...); Връзките придобили огромни тегла в резултат на тази операция са изобразени в розово.
Op2: join(1,2), join(1,3), split(1), split(2); В резултат модулите 4 и 5 станаха "почти" финални.
Op3: BlowUp(4,5,...); Връзките придобили свръхогромни тегла в резултат на тази операция са изобразени в червено.

След всичко това остава само модулите 3, 4 и 5 да се обединят в един сериен модул, а всички останали модули да се разцепят до неутрални. Тъкмо тук става ясно, защо в дефиницията на локалните подсистеми от Фиг.3 се забраняват връзките от 4 или 5 към 2 или 3: наличието на такива връзки би довело до примки със свръхогромни тегла, които по никакъв начин не биха могли да се превърнат във вътрешни връзки.

В седем от тестовите системи (тестове 4-9 и 11 в сегашната версия) имаше поне по една локална подсистема от тип изобразен на Фиг.3pp и Фиг.3ps. Въпреки че аз успях да реализирам без бъгове съответните алгоритми за търсене на тези подсистеми, програмата ми се е провалила в тях тотално заради един странен бъг в иначе тривиалната процедурата записваща операциите в кеша. Разбира се аз отдавна научих основното правило в конкурсите: колкото бъгове и да има програмата, процедурите за записа в изходния файл трябва да се изчистят на всяка цена и преди всичко. Тъкмо затова тази процедура я изпипах в детайли два дена преди крайния срок. Открих един едноредов бъг при записа на join. При разглеждането на процедурата за реализация на BlowUp ми се стори, че подобен бъг има и там. И аз го оправих, заменяйки абсолютно коректния ред с напълно погрешен! Само този фатален бъг ми струваше загубата на 63 точки. При сегашните безбъгови тестващи програми, естественно.

Имаше и още един фатален бъг в моя greedy алгоритм, заради който програмата ми се е издънила в първите 3 теста. За този бъг обаче има рационално обяснение, тъй като целия този greedy алгоритъм писах в последните 3.5 часа преди крайния срок. И бъгът беше вкаран в последните минути, преди изпращането на програмата.

3.3.2. Нелокални подсистеми.

Те са по-прости от локалните: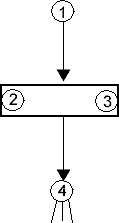

	или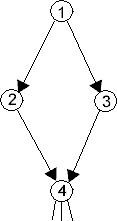
Фиг.5p		Фиг.5s

като в дефиницията им, също като за локалните подсистеми, се изисква отсъствието на обратни връзки от 4 към 2 или 3. С операции, подобни на Op1 и Op2 от Фиг.5, може да се постигне това, че теглото на връзката от 3 към 4 "издухва" теглата на всички останали връзки от и към модул 4, в резултат на което този модул ще стане "почти финален". Аналога на Op3 тук липсва. Обаче, ако намерим още една такава нелокална подсистема, както и неориентиран път от модул 1 към "горния" модул на другата подсистема, който при това не минава нито през модул 4, нито през "долния" модул на другата подсистема, ние можем да намерим гранично решение с баланс N/(N-2) по същия начин, както това бе направено в т.3.2 за два финални модула. В тази схема ние можем, очевидно, и да заменим една от дветте нелокални подсистеми с финален модул.

Трябва да се отбележи, че заради ограничаването на вида на търсения път между двете нелокални подсистеми алгоритъм, който търси две такива подсистеми заедно с допустим път между тях ще има времева сложност O(N*N*(N+броя на връзките)) в най-лошия случай, тъй като алгоритмът трябва да търси път за всяка двойка от намерени нелокални подсистеми (графите в които се търси път за всяка двойка подсистеми не се различават много).

Ето и примера за най-лошия случай, в който нито един от алгоритмите разгледани по-горе няма да намери шампионско решение и ще похарчи време далеч надхвърлящо всички таймаути които биха могли да бъдат наложени от журито (ако то би включило и тест от този тип):

Фиг.6

където "..." означава повтаряне на лявата част на картинката голям брой пъти. Тъй че при реализация на алгоритм търсещ двойка от нелокални подсистеми заедно с хубав път между тях е добре да се сложи таймаут вътре в алгоритъма.

Накрая ще отбележим, че въпреки липсата на граничното решение с баланс N/(N-2) в примера от Фиг.6 може да се намери едно друго гранично решение с баланс N/(N-3), което в дадения конкретен случай ще е и оптимално при голямо (а и при не толкова голямо) N.

По-общо, нека предишните алгоритми за търсене не са открили подсистема или двойка подсистеми, даващи точно гранично решение с баланс N/(N-2), но в системата има паралелни или паралелизуеми двойки модули. Тогава може като кандидат за оптимално или почти оптимално решение да се избере един такъв обект, който при раздуване и обединяване на модули с "дебели" връзки (т.е. тези с огромни тегла) в един сериен модул, ще даде минимален баланс. Аз няма да се спирам тук на детайлите на процедурата за намиране на таково решение ("greedy с раздуване"), а ще премина вече към "чисти" greedy алгоритми, които игнорират всички евентуални възможности за раздуване. А на последния етап, ако има две greedy решения (с раздухване и без него), от тях трябва да се избере онова решение което дава по-малък баланс.

3.4. Greedy алгоритми.

Може да има различни варианти на такива алгоритми. Аз ще опиша тук само един от тях, който на мен ми изглежда по-прост и по-логичен.

1. Разцепваме всички серийни и паралелни модули до неутрални.

2. Сливаме връзките, докато е възможно. По-конкретно, докато в системата има нециклични триъгълници, трансформираме ги по следния начин:

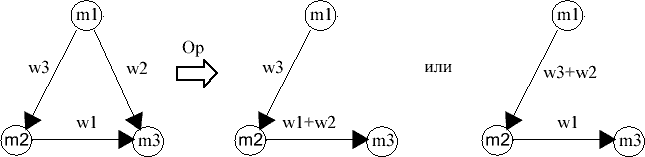Фиг.7

където Op e join(m1,m2), split(m1) или join(m2,m3), split(m2). Очевидно е, че при цикличните триъгълници (т.е. такива, в които стрелката между m1 и m3 е обърната) сливането на двата линка в един не става, затова няма смисъл подобни трансформации да се произвеждат и с тях.

При избора на последователността от трансформируеми триегълници, както и при избора на операцията Ор са възможни различни варианти. Най-простият вариант (който аз реализирах, нямайки време за по-сложни) е итерация по всичките триъгълници в техни "естествен" ред, като винаги се прилага една и съща операция. Като се има предвид целта на този 2-ри етап на сливането на връзки: да концентрира колкото може по-голями тегла в колкото може по-малко връзки, малко по-добра стратегия, която при това няма да заема повече време, е да се избира за всеки триъгълник онази от дветте операции, която дава по-голямо сумарно тегло (w1+w2 или w3+w2). По-сложна greedy стратегия би могла на всеки етап да избира и най-перспективен триъгълник за сливане, т.е. такъв триъгълник, който след сливането ще даде максимално възможно тегло. Очевидно е обаче, че тази стратегия, бидейки реализирана, ще изисква доста повече време за изпълнение, което може да се окаже фатално при тестовете с големи N.

3. Най-накрая прилагаме обикновен greedy алгоритм: докато е възможно намаляване на баланса, избираме измежду външните връзки, които при това не са примки, тази с максимално тегло и съединяваме (с join) серийните модули, които тя свързва. Броят на такива съединения няма да надвиши N, тъй че за да се ускори процеса на избиране на максималната връзка е достаточно да се сортират връзките според тяхното тегло и на всяка стъпка да се избира връзката само измежду първите 2*N връзки с най-големи тегла. Защо 2*N, а не N? Защото е възможна ситуация, когато между всеки два модула свързани с една такава максимална връзка съществува и връзка в обратна посока, чието тегло също е голямо. В такава ситуация само една от дветте връзки може да бъде превърната във вътрешна връзка, докато другата се превръща във външна примка. Важно е да се отбележи също така, че този масив от 2*N елемента трябва да се обновява и да се сортира отново след всяко едно съединяване, тъй като някои от теглата могат да се променят след тази операция.

Доста очевидно е че за системи, които представляват една гора от дървета, "устремени към корена", т.е. такива че всяка тяхна връзка е ориентирана в посока към корена, greedy алгоритъмът дава оптимално решение. Такъв е например тест 1.

Измежду 12 теста на журито (в БАССКОМ варианте) 4-те първи нямат подсистеми, които могат да бъдат "раздувани", т.е. те се оптимизират с greedy алгоритъм. Предполагам, че всеки от тези 4 теста е създаден ръчно, без генератор на случайни графи, защото интуитивно е ясно (без да имам доказателство за това), че вероятността един такъв генератор да създаде граф без паралелни или паралелизуеми модули е малка.

4. Резултати от конкурса такива, каквито би трябвало да бъдат.

Аз написах една проста програмка, която изчислява резултатите от "правилните" тестовете както по формула с log, така и с по-правилната формула от 3-ти коментар. Привеждам сумарните резултати за първите 9 места във "алтернативната" класация. Програмата може да се изтегли (CalcResults.zip), тъй че когото не го мързи, може да направи и пълната класация, допълвайки файла Results.inp с данните за други участници, вземайки ги от таблицата с подобренията на сайта.

А тези, които обичат мазохистични експерименти от вида: "Колко точки бих получил, ако нямаше този гаден мръсен бъг?" могат да се наслаждават, помествайки в началото на Results.inp данни получени от своите пооправени и обезпаразитени програми. Както сигурно се досещате, и аз самият съм голям любител на такива експерименти :).

Ето ги и резултатите:

1.	Евтим Георгиев	71.39
2.	Владимир Недев	70.24
3.	Камен Добрев	56.50
4.	Ангел Джигаров	50.50
5.	Владимир Ралев	48.25
6.	Орлин Колев	45.03
7.	Стоян Йорданов	44.52
8.	Тодор Петков	34.91
9.	Златко Михайлов	28.57

Във файла Results.out има и по-подробна информация: точки получени от всеки един от 11-те теста при 3 варианта на формулата за пресмятане на точките: първи стълб -- вариантът използван от журито, втори -- деклариран в коментара на сайта, трети -- коригиран вариант, деклариран в списанието със задачата. Корекцията е направена, за да не се получават точки само от "stop" във изходния файл. Ако вашата програма подобри максимален резултат от някой тест, това ще бъде отбелязано със стринг от тип "XXX --> YYY" вдясно от таблицата. Тъкмо по-този начин аз открих, че след махане на бъговете от моята програма, тя подобрява най-добрите резултати за следните тестове:

Тест 4	Тест 5	Тест 6	Тест 7	Тест 8	Тест 9	Тест 10	Тест 11
27.101551	113.256767	124.091324	188.980942	226.200485	912.364685	23.206589	357.121307
27.108126	113.258871	124.092373	188.986066	226.202512	992.546932	23.217109	357.123656

В първия ред са предишните рекорди в подобрението на баланса. Във втория -- подобрения от моята програма. Вижда се, че съществени подобрения има само в тест 9. Причина за останалите се дължи очевидно на това, че другите участници, използващи операции на раздуване на връзките, повтаряха комбинацията join/split недостатъчен брой пъти.

Учудващ за мен е фактът, че и моят greedy алгоритм, направен на бърза ръка би се оказал конкурентоспособен в greedy тестове 1-3, ако нямаше бъгове.

5. Нещо за прословутата "еквивалентност".

В заключение искам и аз да се изкажа по един друг "проблем" подет в 1-то писмо на Иван Москов. Другите писма, особено последното, излизат, според мен, извън всякви граници допустими за един интелигентен що-годе човек, и никаква "искреност" на автора не оправдава един порой от помии и закани отправени по адрес на Красимир Манев. Каквито грешки и да е допуснал той.

Тук ще разгледам само тезата, че думата "еквивалентност" в текста на задачата опорочава, заедно с нейната "тривиалност", цялата задача. Що се отнас до "тривиалност", надявам се, че от описанието на алгоритма за нейното решение по-горе всеки може да види, че задачата далеч не е тривиална. А този факт, че тя няма отношение към реални системи -- е от третостепено значение. Ако необходимо условие за конкурсните задачи би било изискването те да описват нещо реално, то трябваше да се изключи и 3-та задача, тъй като звездите не могат да се превключват с ключ. А и самият Малък Принц е само една измишльотина на един неадекватен французин :). Същите "аргументи" важат и за фермера Джон с неговите крави от USACO (виждал ли е някой поне една говореща крава?).

И така -- "еквивалентност". Ето я фразата, която е предизвикала едно от обвиненията в неадекватност:

"Задачата е да се направи програма BALANS.EXE, която по зададена модулна структура на програмна система да намери еквивалентна модулна структура с колкото може по-добър баланс."

За всеки непредубеден читател е ясно, че цялата фраза, заедно с прословутата дума или само думата "еквивалентност" може изобщо да се изхвърли, без да се пострада смисъла на задачата. Това са просто уводни думи и думата "еквивалентност" в тях се употребява не като математически термин, а като един интуитивен образ. Тъй като информацията съдържаща се в не е излишна , то аз при всичките прочити (а на мен ми трябваха не 1.5, а много повече -- е, не съм толкова умен като някои хора ;)) тази дума някак си не я забелязвах, докато не прочетох съответното писмо. И, въпреки това, успях все-пак да разбера смисъла на задачата :).

А сега ще направя едно откритие (което разбира се е един тривиален факт от елементарната теория на множествата преподавана на 1 курс): оказва се че върху всяко едно безкрайно множество (каквото е и множеството на всички "програмни системи") съществуват безброй много релации на еквивалентност! А не някаква си една Еквивалентност спусната на това множество от Господа. Има, в частност и безброй много релации на еквивалентност за които прословутата фраза е коректна, когато думата еквивалентност в нея се интерпретира в точен математичен смисъл, а не само като интуитивен образ. С други думи базовите операции join и split никога не извеждат която и да е система от нейния клас на еквивалентност. Измежду тези безброй много коректни еквивалентности има най-слаба или тривиална (т.е. даваща > едно единствено множество в разбиването, породено от тази еквивалентност). А също така има и най-силна (разбиваща на най-малки множества), която се описва формално като еквивалентност, породена от операциите join и split. По-нагледно и конструктивно тази еквивалентност може да се формулира по следния начин. Ако програмните системи се представят като върхове на един безкраен граф, ориентираните ребра на който се определят от операциите join/split (по-точно: реброто от X към Y съществува тогава и само тогава, когато съществува операция join или split, превръщаща X във Y) тогава X е еквивалентно Y (спрямо тази най-силната релация на еквивалентност) тогава и само тогава, когато X и Y принадлежат на една и съща компонента на свързаност на съответния граф. Или, с други думи, когато между X и Y съществува неориентиран път във този граф.

Между другото, ако в еквивалентността, дефинирана от доц. Красимир Манев в неговия отговор на 1-то писмо се замени думата "ориентиран" с "неориентиран", то така модифицираната еквивалентност ще даде още един пример на еквивалентност съвместима с базовите операции join и split. Това е очевидно, тъй като тези операции не извеждат фрагментите извън техните компоненти на свързаност. Т.е. всеки фрагмент се намира след прилагането на една операция в същата компонента на свързаност на която той принадлежи преди операцията. Разбира се тази еквивалентност е много по-слаба от еквивалентността породена от базовите операции.

6. Заключение.

Накрая искам да благодаря на доц. Красимир Манев, който е направил граматични поправки в горния текст, заменяйки в него, в частност, различните чуждици от английски и от руски произход със еквивалентни български думи. Без да промени при това нито една дума от моя текст по цензурни съображения.
Също така той е уточнил някои от дефинициите дадени в текста и ме накара да добавя разяснение към един прекалено лаконичен пункт.

За въпроси можете да ни пишете на адрес: konkurs@musala.com.

Supported by Musala Soft Ltd.

Коментари към 3-та задача В.Молотков